Dialectics and Math: A Synthesis

A basic analysis on how two seemingly distant concepts are related.

A synthesis: the resulting tension from a thesis and its antithesis. In formal mathematics, proofs are materialized over a bedrock of previously constructed axioms. In a way, arriving at a truth in math could be dialectical in nature. You have a statement A, its consequences. Then, you have a negation of A, and its consequences. The relation of A and its negation tells us whether the statement is correct, but it does not arrive at a new statement or a synthesis. So what could be done? Is this the end of dialectics and its relation to math?

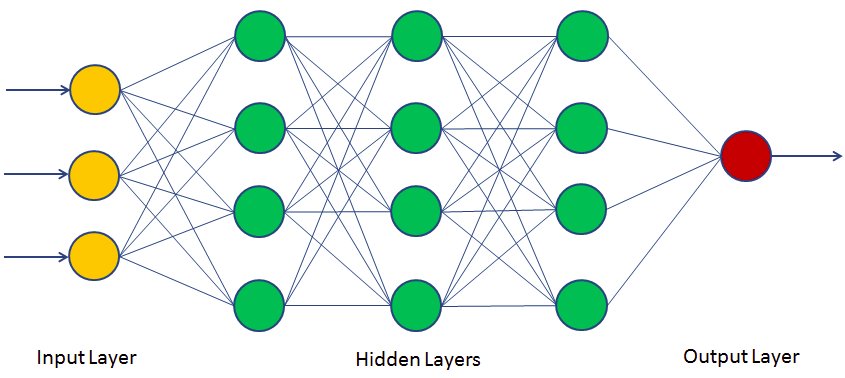
Neural networks provide us a vehicle in which formal math can be conducted in a dialectical nature. To begin to understand what this even means, we have to look at a model of a neural network.

We can begin to analyze a neural network by dividing it into vertical layers. The input layers, are where your ‘variables’ are. This can be images, text, statistics, anything that is discretized can be funneled through this layer. The hidden layers are where the information is piped and transformed via non-linear functions. The easiest way to explain this, is given the equation:

                      y = W1(X1) + W2(X2) + W3(X3)

The W’s, or the weights, are tweaked within the hidden layer. Then, this information is piped into the output layer which contains an activation function. The details and specifics of an activation function are unnecessary.

So, how is this complicated diagram related to dialectics in any comprehensible way? It’s actually quite simple. Marx analyzed the world in terms of the relation of things: the forces and relations of production. The individual neuron in a neural network is completely useless to analyze, and tells us nothing about the structure or process of the network itself. However, if we look at the neuron, and its relation to the other neurons, we gain an immense amount of information. The activation function, the nonlinear transformations, all tell us infinitely more about how the system operates than anything else.

But, this is a trivial way to analyze how dialectics and math are related. I think we could dig a little deeper.

Albert Lautman, a French philosopher, developed mathematics as an expression of opposing themes or notions. Brendan Larvor details how Lautman created this new vision of mathematics in his paper, Albert Lautman: Dialectics in mathematics. The opposing mathematical terms (continuous/discontinuous, global/local, finite/infinite, symmetric/anti-symmetric) are “dialectical ideas” that “envisage possible relations between such pairs of dialectical notions”.

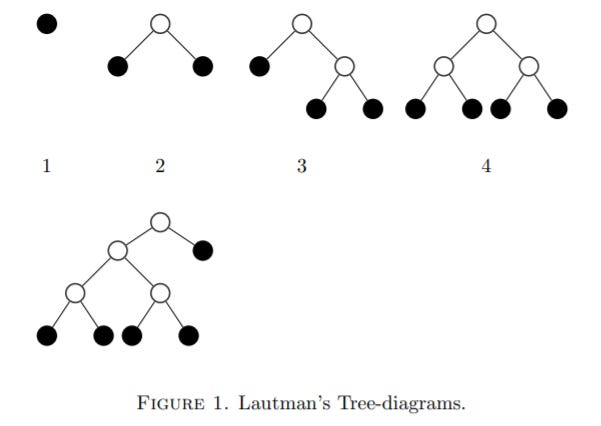
We could be a bit brave and say that the fundamental conceptualization of a “number” is a dialectical process. Lautman claims in his paper, Essay on the notions of structure and existence in mathematics, that the iterations of ‘one’ and a ‘pair’ produce ‘idea-numbers.’ The idea that the natural numbers are a synthesis of one and two is illustrated in figure 1.

It’s hard to look at math and not see it as the philosophy it is. Math is a web woven by ideas and concepts, of which the connections between them give us its material applications to the real world.